Opting for a distributed solution of a problem is mostly motivated by two goals: resilience to failures (via redundancy) and better response time. In this post we will focus on the former. More specifically, we will investigate the conditions necessary to maintain a consistent distributed key-value store.
CAP
From the theoretical side, any possible solution is limited by the so-called CAP theorem. Informally, the theorem states that in an asynchronous network no database can remain
- Consistent and
- Available when
- Partitioning of the network is possible.
A realistic environment of a distributed system must assume that server failures are possible and thus that there is no reasonable fix bound on the time needed to exchange messages between two servers. And while some may find the formulation of the theorem ambiguous, its inevitable corollary is that a distributed database cannot guarantee consistency of replicas and availability of read/write operations at the same time.
Consensus
Leslie Lamport’s Paxos protocol demonstrates the feasibility of maintaining consistency whenever a majority of servers is functioning. The above theorem thus states that any distributed system using the protocol cannot be always available. But there are some highly-available solution apart of Paxos.
Etcd
Etcd is an always-consistent highly-available key-value data store. The consistency is maintained by a majority consensus (quorum). The quorum is established and maintained by the Raft algorithm, i.e. Raft maintains a consistent replicated log among servers, each of which executes the commands stored in the log on the key-value store. As any other consensus protocol, Raft requires that among n servers at most f=⌊(n-1)⁄2⌋ is faulty. If more than f servers become faulty Raft times out all write operations but the read operations may work if consistency is not required.
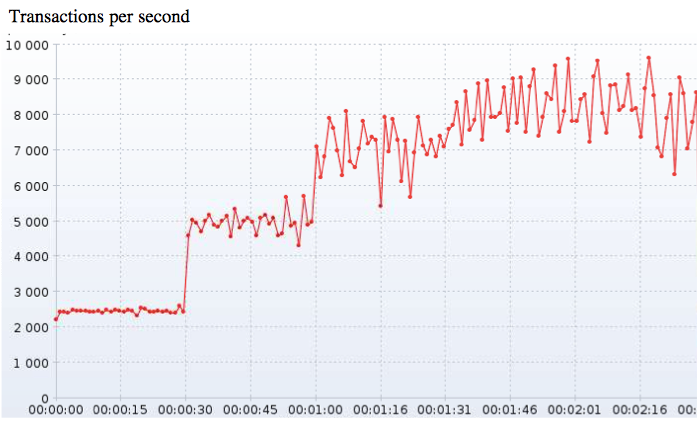
Maintaining consistency is expensive even if only the possibility of partitioning has to be appreciated. Rather than describing the algorithm itself it might be more illustrative to show performance results of running etcd in real application. The figure below depicts the transaction throughput in a 5-node cluster.
The script that measured the performance increased the load in three steps: first a 2500 transaction was sent every second (for 30 seconds), then 5000 for another 30 seconds and then 10000. The data in the plot then report how many transaction successfully finished each second.
Leader Election
Partitions of the cluster are handled by a coordinated replication, i.e. a leader is elected who is responsible for all communication (both within the cluster and with the outside world). In the case of such a partition that separates the leader from most of the nodes, a new leader is elected. The leader election starts whenever the communication between the leader and a follower is lost for more than a randomly chosen time period called election timeout. After the timeout, the follower begins the election by broadcasting the request for vote. Everyone votes for the server that send the request first and the new leader is the server with a majority of votes. Together with the transaction throughput, the performance of leader election are the most important metrics to measure for a consensus protocol.
The graphs above show the time to detect and replace a crashed leader. Each line represents 1,000 trials (except for 100 trials for “150–150 ms”) and corresponds to a particular choice of election timeouts; for example, “150–155 ms” means that election timeouts were chosen randomly and uniformly between 150 ms and 155 ms. The steps that appear on the graphs show when split votes occur (the cluster must wait for another election timeout before a leader can be elected).
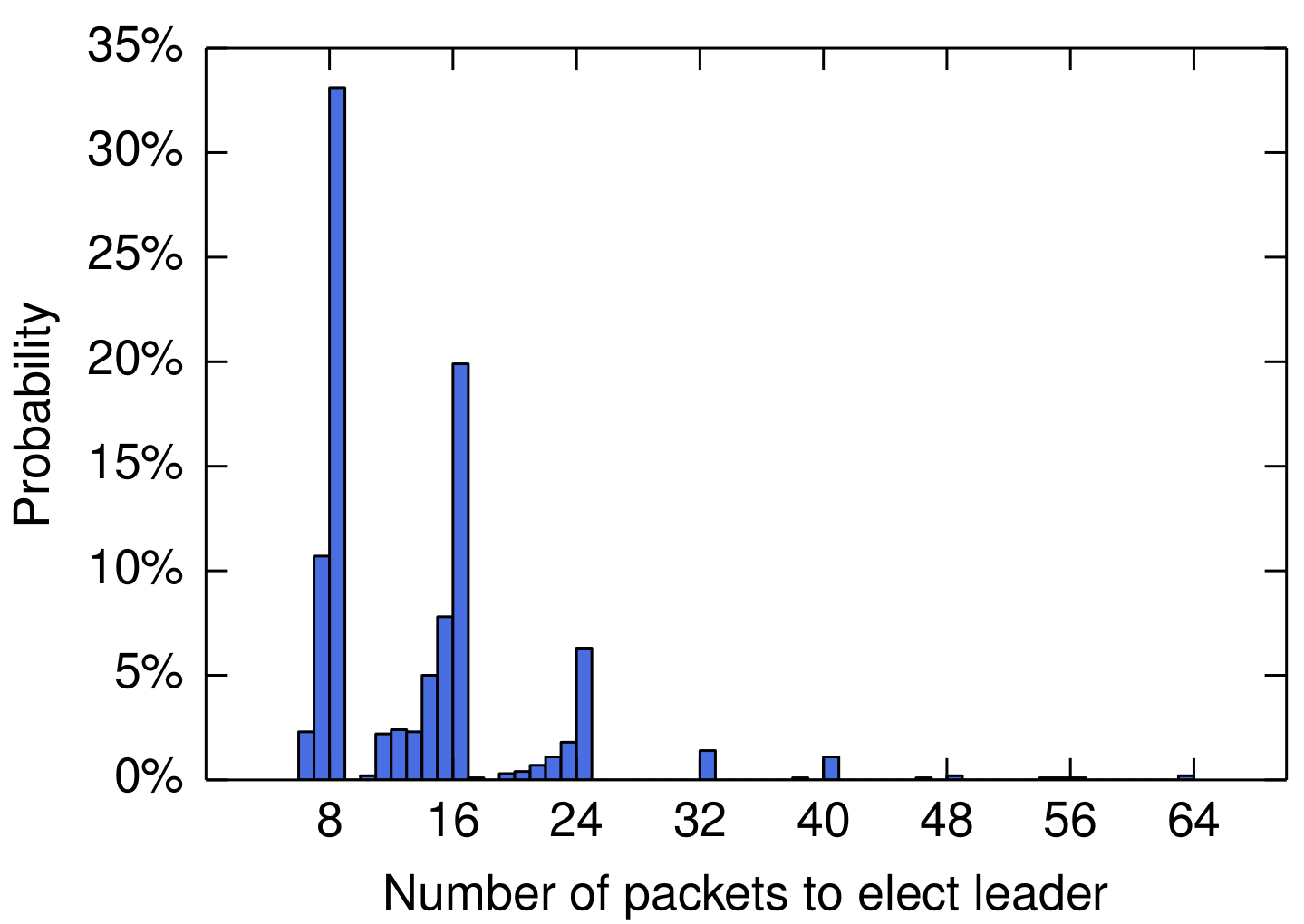
Finally, above is the distribution of the number of packets needed to elect a leader. The figure shows the number of packets sent to elect a leader in the 150–200 ms case. The minimum number of packets is six, representing a single node dispatching requests to the other four nodes and receiving votes from the first two. The plot clusters around multiples of eight: traces under eight represent the first node timing out and winning the election, traces between 8 and 16 represent two nodes timing out before a leader is elected.
Problem Definition
Let us assume that our servers need to share certain configuration. The servers can be restarted, thus becoming temporarily unavailable, and the network can have arbitrarily long delays. The stored data should be available whenever at least one server is alive. Some data must be consistent but other data suffice in possible stale version.
Case 1: Consistency of Logs
Some servers store logs data as a single continuous string. It is required that the logging information is extracted from this string, started from the last extraction point up until the last log. Each log must be accepted for exactly once. We can thus generalise the problem to implementing the following function:
string getLastLog( Server s, string rawLogs )
- the string
rawLogsis a sequence of log information, i.e. <(p1, t1, ..), .. , (pn, tn, ..)> - the function returns a suffix
lastLogsofrawLogssuch thatlastLogs=<(pi, ti, ..), .. , (pn, tn, ..)>, where ti-1<ts and ti >= ts, and ts is the time-stamp of the last retrieval - the function mus be thread-safe in accepting each log at most once regardless the number of concurrent calls of the function
Case 2: Quorum-less access
It is required that the configuration data that need not be consistent can be retrieved and stored even when the quorum cannot be established.
- The get operation returns a value that was either last written by another node (while under quorum), or by this node (possibly without quorum).
- The set operation remember the the new value and stores is when the quorum is reestablished.
Candidate: Etcd
The Etcd has limits in solving both the above cases:
- The CAS operation is implemented as a set operation which specifies the expected previous value that returns either a Boolean value, an exception, or an error. Yet when exception/error is returned we have no guarantees regarding the value in the data store, e.g. the request may have timed out, but afterwards was accepted by Raft and subsequently reflected in the data store.
- Etcd does allow get to operate without quorum but only if the leader is working (any or indeed all other servers may fail). The set operation is not allowed without quorum.
Requirements for Sufficient Solution
Three interface function are required and while the concrete implementation can vary we specify it exactly to avoid confusion.
type Response = { bool valid, bool timeout, string value }
Response get( string key, bool consistent, bool blocking )
consistent=truethe returned value was stored on a majority of servers at the time when this request was accepted by the consensus protocolconsistent=falsethe returned value is the most recent value stored on the server that first received this request (other servers may have different value)blocking=truethe function returns only after the desired data is retrievedblocking=falsethe function may timeout
void set( string key, string value, bool consistent, bool blocking )
consistent=truethe new value is accepted by a majority of servers and until anothersetfor the samekeyis requested, thevaluewill be returned by anyconsistent getconsistent=falsethe new value is accepted by at least the server that first received this request, until anothersetis requested at this server, thevaluewill be returned; furthermore once quorum is established theconsistent setguarantees will be assumed
Response swap( string key, string new_value, string old_value, bool blocking )
consistentby defaultblocking=truethe function returns only after the quorum is established, the function returns true if theold_valuewas stored under key at the time of accepting this request on a majority AND thenew_valuewill be returned by any consistent get until the value is rewritten; most importantly no other value can be returned by get betweenold_valueandnew_value. Ifold_valuewas not stored under key, the function does not modify the data store and returnsfalse.blocking=falsesame guarantees as above but the function may timeout without modifying the data store.
Any distributed data-store conforming to the above requirements would be sufficient to solve the above problem. Yet the cost of consistency is high and only a few data-stores offer adequate protection from partitioning. Etcd seems the closest candidate but its functionality needs to be extended.